Sistemi Intelligenti
universityProfessoressa: Cristina Baroglio
Terminologia
- AI coniato da John McCarthy
- Dato, simbolo grezzo
- Informazione, un dato elaborato
- Conoscenza, campo di informazioni correlate tra loro
- Automazione,
- Autonomia,
Automazione
Campo in cui l’informatico piu' in generale viene applicata
- automazione del calcolo
- automazione contabile
- automiazione della ricerca di informazione, motori di ricerca
Tratta di programmare un supporto a fare ogni passo, applicabile in domini fortemente ripetitivi
Autonomia
Svolta da un agente artificiale che risolve un compito
- non viene indicato passo passi il modo per raggiungere l’obiettivo
- vengono forniti solo compiti ad alto livello
Utile nei problemi:
- non deterministici
- in cui c’e' molteplicita' di soluzioni
- con dati di natura simbolica
- si ha una conoscenza ampia e completa
- dove l’informazione e' parzialmente strutturata
Comprensione
Output attesi \(\implies\) comprensione? John R. Searle
Test di Turing
- test per definire se un computer e' intelligente, o se un programma lo e'
- in linguaggio naturale
- per T lo e' quando inganna l’uomo, imitando il comportamento umano
- un computer che deve passare il test non eseguira' gli ordini direttamente, in quanto questi vanno filtrati rispetto alle capacita' di un umano
The Imitation Game
Captcha
Completely Automated Public Turing-test to tell Computers and Humans Apart
Turing test inverso
Strong & Weak
- studio del pensiero e del comportamento umano, scienze cognitive
- riprodurre l’intelligenza umana
- risolvere problemi che richiederebbero intelligenza degli umani per essere risolto
- non ci importa come l’umano ragiona, importa come risolvere il problema
- task-oriented
Agente - Environment
L’agente é immerso in un ambiente e svolge in ciclo esecutivo:
- Percepisce
- Delibera
- Agisce
L’ambiente definisce cosa e' efficace e cosa non lo e'. questo in base agli attuatori degli agenti possono essere posti in questo ambiente. L’ambiente, in base a come si evolve nel tempo della percezione e deliberazione, puo' essere:
- statico
- dinamico
Inoltre si puo' distinguere un ambiente:
- deterministico
- possibile prevedere in che stato un azione sposta l’ambiente
- stocastico
- non e' possibile prevedere in tutti i casi lo stato in cui ci si trovera' dopo un azione
Agente Autonomo
- ha capacitá di azione
- riceve compiti ad alto livello
- esplora alternative, numero esponenziale di possibilitá da esplorare
- riconosce
- se una strada non puó portare a una soluzione
- un strada giá esplorata
Un AA rimane un programma, non fará ció che non é programmato a fare
Il cuore dell’agente é la funzione deliberativa
- un agente é razionale se opera per conseguire il successo
- questo é possibile con una misura di prestazione utilizzata come guida
La razionalitá ottimizza il risultato atteso
- possono intercorrere fattori ignoti o imprevedibili
Paradigma Dichiarativo
- imperativo: how, sequenza di passi
- dichiaritivo: what, si sfrutta una
knowledge base- il cuore é il Modulo dichiarativo che utilizza l’informazione dalla percezione e la propria knowledge base
Quindi:
- un programma, risolutore, produce un altro programma che risolva una particolare istanza del mondo
Risoluzione Automatica
- nella realtá di riferimento si astrae utilizzando degli stati
- astraendo si lascia solo una descrizione essenziale
- discreti
- tra questi ci saranno stati target e stati di partenza
- la realtá transisce da uno stato all’astro tramite azioni
- le azioni hanno effetto deterministico
- il dominio della realtá é statico
- l’algoritmo di ricerca determina una soluzione
- permette di raggiungere da uno stato iniziale uno stato target
- una soluzione é un percorso del grafo degli stati
- utilizza:
- descrizione del problema
- metodo di ricerca
- permette di raggiungere da uno stato iniziale uno stato target
Fornendo una situazione iniziale e una situazione da raggiungere, appartenenti allo stesso dominio, l’agente deve trovare una soluzione
Problemi
Un problema puó essere definito formalmente come una tupla di 4 elementi
- Stato iniziale
- Funzione successore
- Test Obiettivo
- Funzione del costo del cammino
Aspirapolvere
Gioco del 15
Problema di ricerca nello spazio degli stati
- stato iniziale, qualsiasi
- funzione successore, spostamento di una tessera adiacente allo spazio vuoto nel suddetto
- test obiettivo, verifica che la stato sia quello desiderato (tabella ordinata)
- costo del cammino, ogni passo costa 1 e il costo del cammino é il numero di passi che lo costituiscono
-
Euristiche
- \(h_1\) numero delle tessere fuori posto (rispetto alla configurazione goal)
- \(h_2\) distanza di Manhattan
- in particolare \[\sum_{\forall c}d_{\text{man}}( c)\]
8 Regine
Posizionare 8 regine su una scacchiera \(8\times8\) in modo che nessuna sia sotto attacco
- generalizzabile con \(N\) regine su una scacchiera \(N\times N\)
Algoritmi
Ricerca non informata - Blind
Costruiscono strutture dati proprie utilizzate nella soluzione di un problema
- alberi o grafi di ricerca
- in un albero uno stato puó comparire piú volte
Ogni nodo rappresenta uno stato, una soluzione é un particolare percorso dalla radice ad una foglia
- i nodi figli sono creati dalla funzione successore
- questi sono creati mantenendo un puntatore al padre
Gli approcci sono valutati secondo
- completezza
- ottimalitá
- complessitá temporale
- complessitá spaziale
Gli alberi vengono esplorati tramite Ricerca in Ampiezza e Ricerca in Profonditá
Nello studio di queste ricerche si considerano:
- \(d\) profondita' minima del goal
- \(b\) branching factor
Un goal a meno passi dalla radice non da' garanzia di ottimalita', in quanto vanno considerati i costi non il numero di passi. Il costo e' una funzione monotono crescente in relazione alla profondita'.
-
Ricerca in Ampiezza
\(O(b^{d+1})\)
- complessitá sia spaziale che temporale
- esponenziale, non trattabile anche con \(d\) ragionevoli
-
Ricerca Costo Uniforme
Cerca una soluzione ottima, che non in tutti i problemi corrisponde a il minor numero di passi. La scoperta di un goal non porta alla terminazione della ricerca. Questa termina solo quando non possono esserci nodi non ancora scoperti con un costo minore di quello gia' trovato.
La ricerca puo' non terminare in caso di
no-op, che creano loop o percorsi infiniti sempre allo stesso stato. Quindi: \(\text{costi} \ge \epsilon > 0\)- \(\epsilon\) costo minimo
\[O(b^{1+\lfloor \frac{C^{*}}{\epsilon} \rfloor})\]
- \(C^{*}\) costo soluzione ottima
-
Ricerca in Profonditá w/ Backtracking
Si producono successori su successori man mano, percorrendo in profondita' l’albero. In fondo, in assenza di goal, viene fatto backtracking cercando altri successori degli nodi gia' percorsi.
- viene esplorato un ramo alla volta, in memoria rimane solo il ramo che sta venendo esplorato
- piu' efficiente in utilizzo della memoria
-
Ricerca in Profonditá w/o Backtracking
Si esplora espandendo tutti i figli ogni volta che viene visitato un nodo non goal
- viene utilizzato uno
stack(LIFO)
- viene utilizzato uno
-
Iterative Deepening
Ricerca a profonditá limitata in cui questa viene incrementata a ogni iterazione
- cerca di combinare ricerca in profonditá e in ampiezza
- \(\textsc{time}= O(b^d)\)
- \(\textsc{space}= O(b\cdot d)\)
- completa
- ottima quando il costo non é funzione decrescente delle profonditá
- cerca di combinare ricerca in profonditá e in ampiezza
-
Ricerca Bidirezionale
2 ricerche parallele
- forward dallo stato iniziale
- backwards dallo stato obiettivo
Termina quando queste si incontrano a una intersezione. Il rischio é che si faccia il doppio del lavoro e che non convergano a metá percorso ma agli estremi
- \(\textsc{time}= O( b^{\frac{d}{2}})\)
Ricerca informata
Si possiedono informazioni che permettono di identificare le strade piú promettenti
- in funzione del costo
Questa informazione é chiamata euristica \(h(n)\): Il costo minimo stimato per raggiungere un nodo preferito di \(n\)
-
Greedy
- costruisce un albero di ricerca
- mantiene ordinata la frontiera a seconda di \(h(n)\)
Ma l’euristica puó essere imperfetta e creare dei problemi. Questa strategia considera solo informazioni future, che riguardano ció che non é ancora stato esplorato.
-
A*
Combina informazioni future e passate:
- Greedy e Ricerca a costo uniforme
Utilizza una funzione di valutazione: \(f(n) = g(n) + h(n)\)
Dove \(g(n)\) é il costo minimo dei percorsi esplorati che portano dalla radice a \(n\)
I costi minimi reali sono definiti con: \(f^{\star}(n) = g^\star(n) + h^\star(n)\)
- definizione utilizzata nelle dimostrazioni
\(A^\star\) é ottimo quando
- tutti i costi da un nodo a un successore sono positivi
- l’euristica \(h(n)\) é ammissibile
Ammissibilitá
- \(\forall n: h(n) \le h^\star(n)\)
- ovvero l’euristica é ottimistica
Nel caso di ricerca in grafi \(h(n)\) deve essere anche monotona consistente per garantire l’ottimalitá
- vale una disuguaglianza triangolare
- \(h(n) \le c(n,a,n') + h(n')\)
- \(\textsc{nb}\) tutte le monotone sono ammissibili ma non vale il viceversa
Inoltre é ottimamente efficiente
- espande sempre il numero minimo di nodi possibili
Ma \(\textsc{space}=O(b^d)\)
Euristiche
Calcolo della Bontá
Per decidere tra 2 euristiche ammissibili quale sia la piú buona
- confronto sperimentale
- confronto matematico
Si considera la dominanza
- \(\forall n : h_2(n) \le h_1(n)\le h^\star(n)\)
- restituisce sempre valore maggiore rispetto all’altra
- una euristica dominante sará piú vicina alla realtá
Si puó costruire una nuova \(h(n) = \max(h_1(n),\dots,h_k(n))\) dominante su tutte quelle che la compongono
Si valuta la qualitá dell’euristica (sperimentalmente) con il branching factor effettivo \(b^\star\)
- si costruisce con gli \(N\) nodi costruiti nella ricerca un albero uniforme
- \(b^\star\) piccolo \(\rightarrow\) euristica efficiente
Ricerca Con Avversari
Informazione puo' essere
- perfetta
- imperfetta
Effetti delle scelte
- deterministici
- stocastici
La ricerca in questo ambito si basa su delle strategie basate su punteggi dati dagli eventi. Alcuni giochi sono anche a somma zero.
Teoria delle Decisioni
Dall’Economia, poi traslata in algoritmi nell’ambito dell’IA.
- approccio maximax - ottimistico
- approccio maximin - conservativo
- approccio minimax regret - minor regret
-
Minimax
Minimaxe' un algoritmo pessimista nel senso che simula cheMinsi muova in modo perfetto.- ricerca in profondita', esplora tutto l’albero ma non mantiene tutto in memoria
Nella simulazione dell’albero di gioco si hanno i due attori
MaxMin
L’algoritmo fa venire a galla i costi terminali dei rami del gioco, in quanto per guidare la scelta
Maxdeve poter scegliere tra i nodi a se successivi.La funzione utilita' valuta gli stati terminali del gioco, agisce per casi sul nodo \(n\) in maniera ricorsiva \(\text{minimax-value}(n)\):
- se \(n\) terminale
- \(\text{utility}(n)\)
- se \(n\)
Max- \(\text{max}_{s \in succ(n)}(\text{minimax-value}(n))\)
- se \(n\)
Min- \(\text{min}_{s \in succ(n)}(\text{minimax-value}(n))\)
def minimaxDecision(state): # returns action v = maxValue(state) return action in succ(state) with value == v def maxValue(state): # returns utility-value (state) if (state.isTerminal()): return utility(state) v = sys.minint for (a,s) in succ(state): # (action,successor) v = max(v, minValue(s)) return v def minValue(state): if (state.isTerminal()): return utility(state) v = sys.maxint for (a,s) in succ(state): v = min(v, maxValue(s)) return v- \(\textsc{space} = O(bm)\)
- \(\textsc{time} = O(b^{m})\)
-
Potatura alpha-beta
Si agisce potando le alternative che non potranno cambiare la stima corrente a quel livello. La potatura viene fatta in base all’intervallo \(\alpha \cdots \beta\) dove:
- \(\alpha\) e' il valore della migliore alternativa per
Maxnel percorso versostate - \(\beta\) e' il valore della migliore alternativa per
Minnel percorso versostate
Se il \(v\) considerato e' fuori da questo intervallo allora e' inutile considerarlo.
def alphabetaSearch(state): # returns action v = maxValue(state, sys.minint, sys.maxint) return action in succ(state) with value == v def maxValue(state, alpha, beta): # returns utility-value (state) if (state.isTerminal()): return utility(state) v = sys.minint for (a,s) in succ(state): # (action,successor) v = max(v, minValue(s, alpha, beta)) if (v >= beta) return v alpha = max(alpha, v) return v def minValue(state, alpha, beta): if (state.isTerminal()): return utility(state) v = sys.maxint for (a,s) in succ(state): v = min(v, maxValue(s, alpha, beta)) if (v <= alpha) return v beta = min(beta, v) return vQuesto algoritmo e' dipendente dall’ordine di esplorazione dei nodi, alcune azioni killer move permettono di tagliare l’albero subito e non sprecare passi.
- \(\textsc{time} = O(b^{m/2})\)
- nel caso migliore
- se l’ordine e' sfavorevole e' possibile che non avvengano potature
Esistono tecniche di apprendimento per le killer move, il sistema si ricorda le killer move passate e le cerca nelle successive applicazioni. Queste tecniche sono studiate in quanto la complessita' continua a essere troppo alta per applicazioni
RealTime:- trasposizioni
- permutazioni dello stesso insieme di mosse
- mosse che portano allo stesso stato risultante
- vanno identificate ed evitate
- classificazione stati di gioco
- per motivi di tempo vanno valutati come foglie nodi intermedi
- va valutata una situazione intermedia (orizzonte)
- valutazione rispetto alla facilita' di raggiungere una vittoria
- attraverso un classificatore sviluppato in precedenza
- quiescenza dei nodi
- se mantiene la propria valutazione bene nei continuo
- non ribalta la valutazione nel giro di poche mosse
- \(\alpha\) e' il valore della migliore alternativa per
Soddisfacimento di Vincoli
CSP - Constraint Satisfaction Problems
- serie di
variabilidi dati dominii vincolo, una condizione- é soddisfatto con una dato
assegnamentoche per essere una soluzione deve essere- completo, tutte le variabili sono assegnate
- consistente, tutti i vincoli sono rispettati
- é soddisfatto con una dato
I problemi sono affrontati con approcci diversi in base alle caratteristiche del dominio (valori booleani/discreti/continui)
Algoritmi
-
Generate and Test
Bruteforce
- genera un assegnamento completo
- controlla se é una soluzione
- se si
returnaltrimenticontinue
É estremamente semplice ma non é scalabile.
-
Profonditá con Backtracking
Si esplora l’albero delle possibili assegnazioni in profonditá. Si fa backtracking quando si incontra una assegnazione parziale che non soddisfa piú le condizioni Il problema é che in
CSPilbranching factoré spesso molto alto, producendo alberi molto larghi. Dati \(n\) variabili e \(d\) media del numero di valori possibili per una variabile:- il
branching fatoral primo livello, \(n \cdot d\) - … al secondo, \((n-1)\cdot d\)
- l’albero avrá \(n! \cdot d^{n}\) foglie
Questo é migliorabile con la tecnica del fuoco su una singola variabile a ogni livello dell’albero, questo in quanto i
CSPgodono della proprietá commutativa rispetta all’ordine delle variabili. Questo permette di rimuove il fattoriale nel numero di foglie.Uno dei difetti di questo approccio é il
Thrashing, riconsiderando assegnamenti successivi che si sono giá dimostrati fallimentari durante l’esplorazione. - il
-
Forward Checking
Approccio locale di propagazione della conoscenza. Si propagano le scelte delle variabile ai vicini diretti, restringendo il dominio di questi vicini. In caso di individuare una inconsistenza se esiste.
-
AC-3
Arc Consistency- McWorth- funziona con vincoli binari
- simile al Forward Checking
Arc Consistencynon é una proprietá sufficiente a garantire l’esistenza di una soluzione
def AC-3(csp): // returns CSP ridotto queue = csp.arcs while queue != empty: (xi,xj) = queue.RemoveFirst() if (RemoveInconsistentValues(xi,xj)): for (xk in xi.neighbours): queue.Add(xk,xi) def RemoveInconsistentValues(xi,xj): // returns boolean removed = false for (x in Domain[xi]) if (no value y in Domain[xj] consents to satisfy the constraint xi,xj): Domain[xi].delete(x) removed = true return removed
-
Back-Jumping
Risolve i limiti del tradizionale
Backtracking Cronologico, che torna passo per passo indietro senza sfruttare i vincoli. Si viene guidati dal Conflict Set. Si fa backtracking a una variabile che potrebbe risolvere il conflitto.- questi
CSsono costruiti tramiteForward Checkingdurante gli assegnamenti
Sia \(A\) un assegnamento parziale consistente, sia \(X\) una variabile non ancora assegnata. Se l’assegnamento \(A \cup \{X=v_{i}\}\) risulta inconsistente per qualsiasi valore \(v_{i}\) appartenente al dominio di \(X\) si dice che \(A\) é un conflict set di \(X\)
Quando tutti gli assegnamenti possibili successivi a \(X_{j}\) falliscono si agisce con il
Back-Jumping- si considera l’ultimo assegnamento \(X_{i}\) aggiunto al
CSdi \(X_{j}\) - viene aggiornato il
CSdi \(X_{i}\)- \(CS(X_{i})=CS(X_{i})\cup (CS(X_{j})- \{X_{i}\})\)
- questi
Euristiche
- di variabile
Minimum Remaining Values- fail-firstGrado
- di valore
Valore Meno Vincolante- lascia piú libertá alle variabili adiacenti sul grafo dei vincoli
Euristiche di scelta e inferenza
- alternanza tra esplorazione e inferenza
- ovvero propagazione di informazione attraverso i vincoli
-
Consistency
Node Consistency- vincoli di aritá 1 soddisfatti
Arc Consistency- vincoli di aritá 2 soddisfatti per ogni valore nel dominio
- un arco é
arc-consistentquando \(\forall\) valore del dominio del sorgente \(\exists\) valore nel dominio della destinazione che permetta di rispettare il vincolo
Path Consistency- 3 variabili legate da vincoli binari
- considerate 2 variabili \(x, y\) queste sono
path-consistentcon \(z\) se \(\forall\) assegnamento consistente di \(x,y \; \exists\) un assegnamento \(z\) tale che \(\{x,z\}\) e \(\{y,z\}\) questi sono entrambi consistenti.
Questi concetti sono generalizzabili con la
k-consistenza- per ogni sottoinsieme di \(k-1\) variabili e per ogni loro assegnamento consistente é possibile identificare un assegnamento per la \(k\text{-esima}\) variabile che é consistente con tutti gli altri.
Un
CSPfortemente consistente puó essere risolto in tempo lineare.
Vincoli Speciali
AllDifferent- test sul numero di valori rimanenti nei domini delle variabili considerate
Atmost- disponibilitá \(N\)
- risorse richieste dalle entitá
- vincoli utilizzati nella logistica
Problema dell’Australia
3 colori per colorare i 7 territori dell’Australia
- {
NA,NT,SA,Q,NSW,V,T} - un territorio deve avere colore diverso da tutti i vicini
Rappresentazione della Conoscenza
Agenti su Conoscenza
Caratterizzati da:
Knowledge Base- generalmente cambia nel tempo
- inizialmente formata dalla background knowledge
Tell- assertAsk- query- ogni risposta deve essere una conseguenza di asserts e background knowledge
Formalismi Logici
Per la rappresentazione di Knowledge Base
- Linguaggio di Rappresentazione
- con cui vengono formate formule ben formate
- la semantica del linguaggio definisce la veritá delle formule
- Modello \(F_n\)
- é un assegnamento di valori ai simboli proposizionali
- permette la valutazione delle formule
- Conseguenza \(\vDash\)
- in generale il lato sinistro é sottoinsieme del destro
- per ogni caso di \(F_{1}\) vale anche \(F_{2}\): \(F_{}_{}_{1} \vDash F_{2}\)
- non é l'implicazione logica, sono su piani diversi anche se sono simili
- in generale il lato sinistro é sottoinsieme del destro
- Equivalenza \(\equiv\)
- \(F_{1} \vDash F_{2} \land F_{2} \vDash F_{1}\)
- Validitá
- o tautologia
- vera in tutti i modelli
- Insoddisfacibilitá
- o contraddizione
- una formula ins. é falsa in tutti i modelli
- Soddisfacibilitá
- formula per il quale esiste qualche modello in cui é vera
- Inferenza \(\vdash\)
- propagazione informazione
- \[\frac{\text{premesse}}{\text{conclusione}}\]
- Algoritmi di Inferenza manipolano inferenze per derivare formule
- correttezza (soundness)
- \(KB \vdash_{i} A \implies KB \vDash A\)
- completezza
- \(KB \vDash_{} A \implies KB \vdash_{i} A\)
- correttezza (soundness)
- Grounding
Semantica
- \(KB_{LP}\vDash P_{LP}\)
Vari approcci:
- Model Checking
- \(n\) simboli, \(2^{n}\) modelli possibili
- Theorem Proving
- basato sull’inferenza sintattica
- quindi sulla manipolazione delle formule
- utilizza le
Regole di Inferenza- contrapposizione, de Morgan, associativitá…
Teorema di Deduzione- date formule \(R,Q\)
- \(R\vDash Q \iff R\implies Q \text{ é una formula valida o tautologia}\)
- \(Q\) é conseguenza logica di \(R\)
- basato sull’inferenza sintattica
Theorem Proving
- Algoritmo di Ricerca (o di inferenza)
- Insieme di regole di inferenza
Risoluzione- disgiunzioni in cui si fattorizzano analoghi e si cancellano i contrari
- il
Modus Ponensne é un caso particolare - si applica a
CNF- \(KB_{\text{LP}} \vdash KB_{\text{CNF}}\)
- si eliminano le biimplicazioni
- si eliminano le implicazioni
- si portano all’interno i
notapplicandode Morgan - si eliminano le doppie negazioni
- si distribuisce
orsull'and
- congiunzioni di clausole (disgiunzioni di letterali)
- \(KB_{\text{LP}} \vdash KB_{\text{CNF}}\)
Teorema: Se un insieme di clausole é insoddisfacibile la chiusura della risoluzione contiene la clausola vuota
- questo é utilizzato nella dimostrazione per refutazione
-
Horn Clauses
Un caso particolare delle clausole.
Una clausola di horn é una disgiunzione di letterali in cui al piú uno é positivo.
ad esempio:
\[\frac{\lnot A \lor \lnot B \lor C}{A \land B \Rightarrow C}\]
\[\frac{\lnot A \lor \lnot B}{A \land B}\]
-
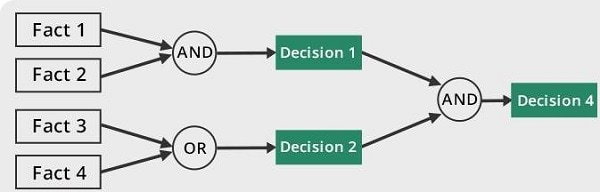
Forward Chaining
Lineare nel numero di clausole
- ogni clausola é applicata al piú una volta
- peró sono applicate clausole inutili per il target
-
Backward Chaining
Parte dalla formula da dimostare e va a ritroso
- piú efficiente del
Forward Chaining - meno che lineare
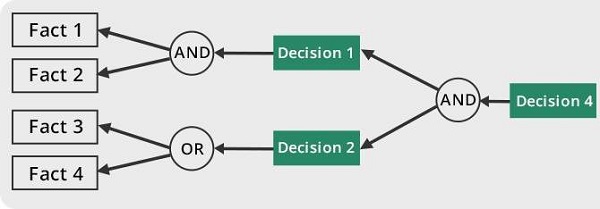
- piú efficiente del